LAMBDA Functions

Common Formulas

LAMBDA, MAP, SCAN, VSTACK, HSTACK, DROP

LAMBDA Overview And Simple Example

LAMBDA functions enable Excel users to create user-defined functions. The following toy example illustrates the general idea. Suppose we often encounter return streams (daily returns, monthly returns, etc.) from which we’d like to calculate an annualized return (in the case where the return stream lasts longer than a year) or a holding period return (if the return stream is a year or less). This is not a hard task in general, but it becomes annoying to tweak existing formulas in order to fit different return frequencies or lengths (e.g., trusting other users of your workbook to alter formulas if the return stream changes from “many years of quarterly data” to “a few months of daily data” ).

Figure 1: Examples Of Different Return Frequencies And Lengths

There are five possibilities we want to include in our function. For return streams lasting longer than a year, we need four cases to handle the four common reporting frequencies (daily, monthly, quarterly, annually). All of the different frequencies will utilize GEOMEAN with a different exponent. For return streams shorter than a year, we only need one case since PRODUCT will work for all frequencies.

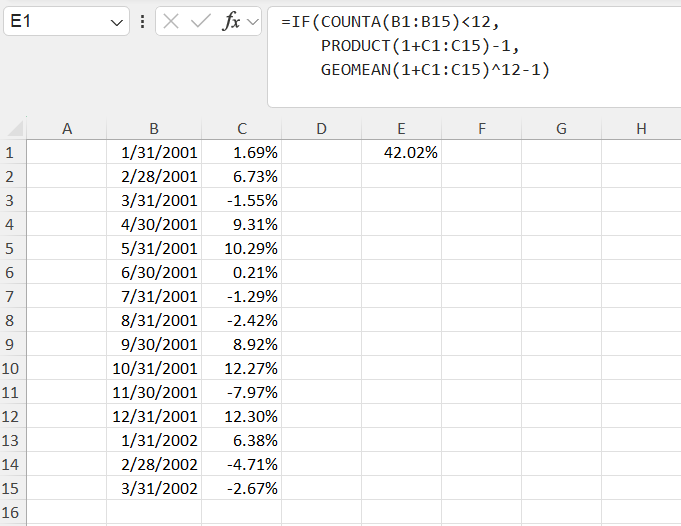
Working from the inside out, we can use a simple IF statement to handle the five cases. For sake of illustration, let’s start with the simplified assumption that we know all return streams will be based on monthly data. Then we only have two cases to consider– if the length of the return stream is greater than 12, we use GEOMEAN, and if the length of the return stream is less than 12, we use PRODUCT. Then our formula is something like =IF(COUNTA(range)<12, PRODUCT(1+range)-1, GEOMEAN(1+range)^12-1).

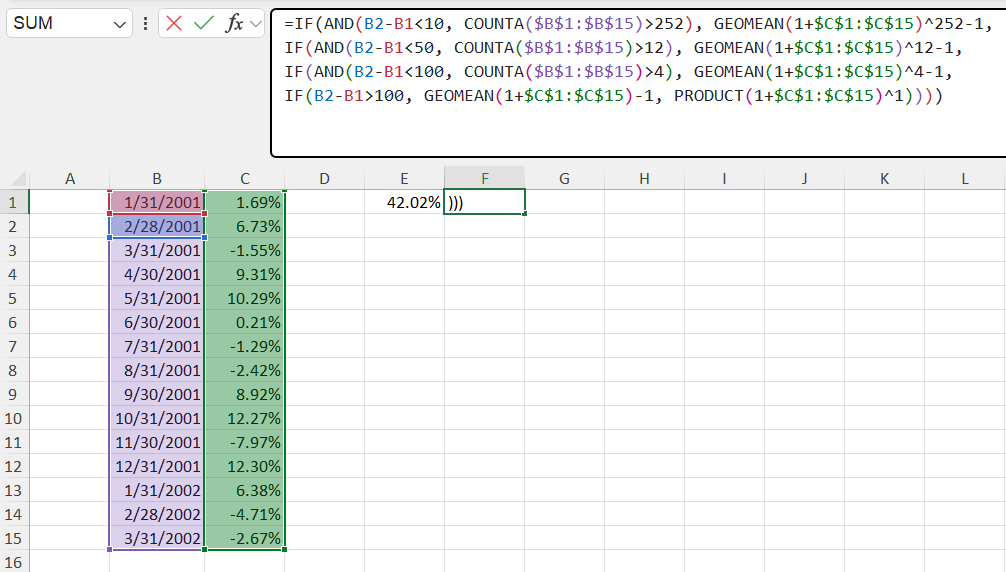
Figure 2: Formula If We Know Return Stream Is “Monthly”

This simplified idea is the frame by which we’ll extend our formula to accommodate other types of return streams. A crude but effective way for Excel to see the frequency which is being reported is to difference the first two dates in our series. Quarterly data will always have more than 50 but less than 100 days between dates, monthly data will always have more than 10 but less than 49 days between dates, etc. Once we figure out the difference between dates, we have the frequency of the return stream. And once we have the frequency of the return stream, we can figure out which formula to use–PRODUCT or GEOMEAN— since we’ll also have the length of the returns. For example, if the difference between the first two dates implies daily returns, and if the number of days in our return stream is longer than 252 (the approximate number of trading days in a year), we annualize our result. The full idea is captured in the code chunk below.


=IF(AND(daterange_2-daterange_1<10, COUNTA(returnrange)>252), GEOMEAN(1+returnrange)^252-1,
IF(AND(daterange_2-daterange_1<50, COUNTA(returnrange)>12), GEOMEAN(1+returnrange)^12-1,
IF(AND(daterange_2-daterange_1<100, COUNTA(returnrange)>4), GEOMEAN(1+returnrange)^4-1,
IF(daterange_2-daterange_1>100, GEOMEAN(1+returnrange)-1, PRODUCT(1+returnrange)^1))))
Figure 3: Accommodating Different Reporting Frequencies

Rather than repeat the same formulas within our IF statement, we can name the results once and then reference the result later within the same formula using LET. For consistent display style, we can also wrap the result in ROUND.

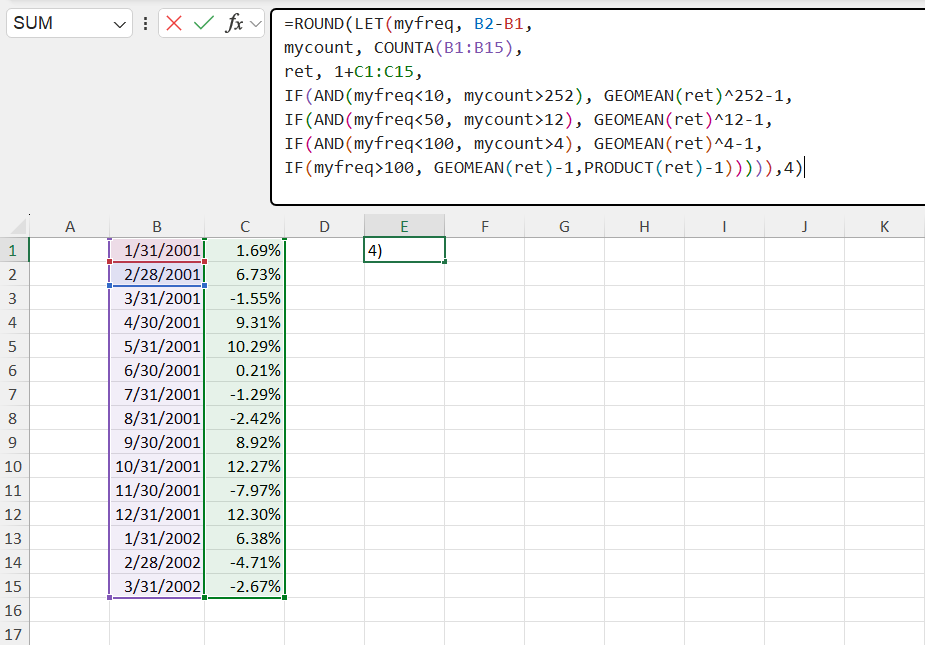
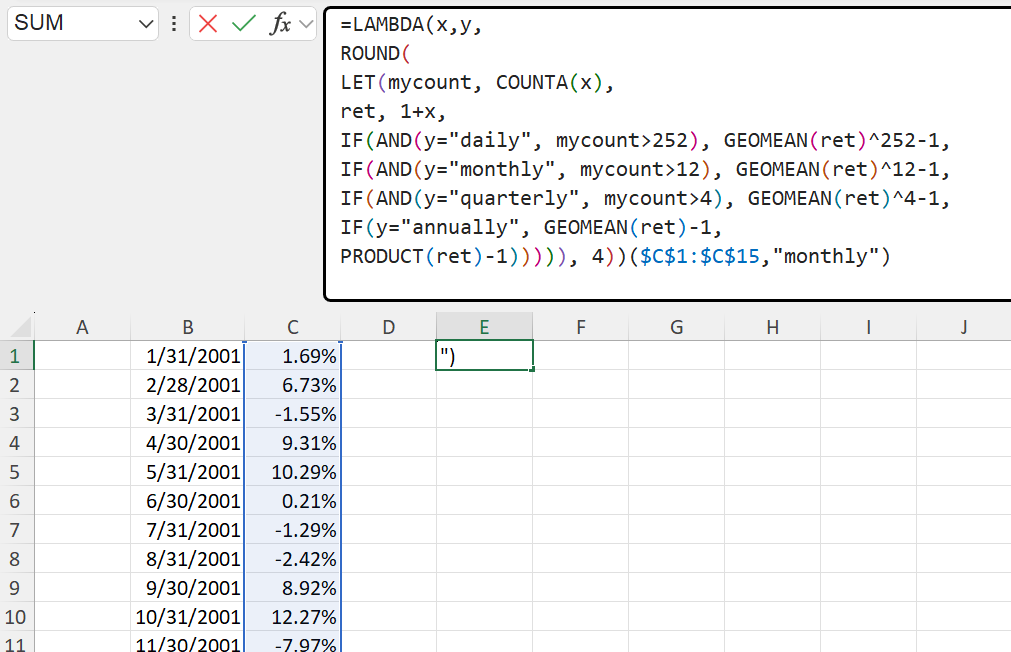
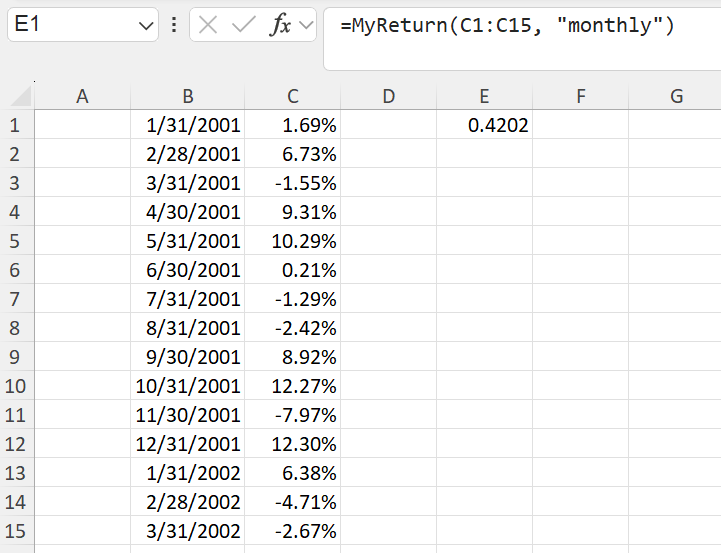
Figure 4: Cleaning Up Formula With LET

We now have a function that achieves our desired result. The downside is that the function is long, and that we must adjust the specifics inside the function (the date range, the return range, the difference in dates) anytime we get a new return stream. This is both inefficient and significantly hinders the auditing of results. This is where LAMBDA comes in. In essence, the LAMBDA function has two parts– a function we want to implement (e.g., the long formula in Figure 4), and the generic “inputs” (e.g., x, y) that we use as dummy variables inside the function we want to implement. A simple LAMBDA implementation below of Figure 4 is shown below. The last part, ($C$1:$C$15,"monthly"), are the specific parameters we run the function on (the x is the $C$1:$C$15, and the y is the "monthly".


=LAMBDA(x,y,
ROUND(
LET(mycount, COUNTA(x),
ret, 1+x,
IF(AND(y="daily", mycount>252), GEOMEAN(ret)^252-1,
IF(AND(y="monthly", mycount>12), GEOMEAN(ret)^12-1,
IF(AND(y="quarterly", mycount>4), GEOMEAN(ret)^4-1,
IF(y="annually", GEOMEAN(ret)-1,
PRODUCT(ret)-1))))), 4))($C$1:$C$15,"monthly")
Figure 5: Crafting A Simple LAMBDA Function

Name Manager

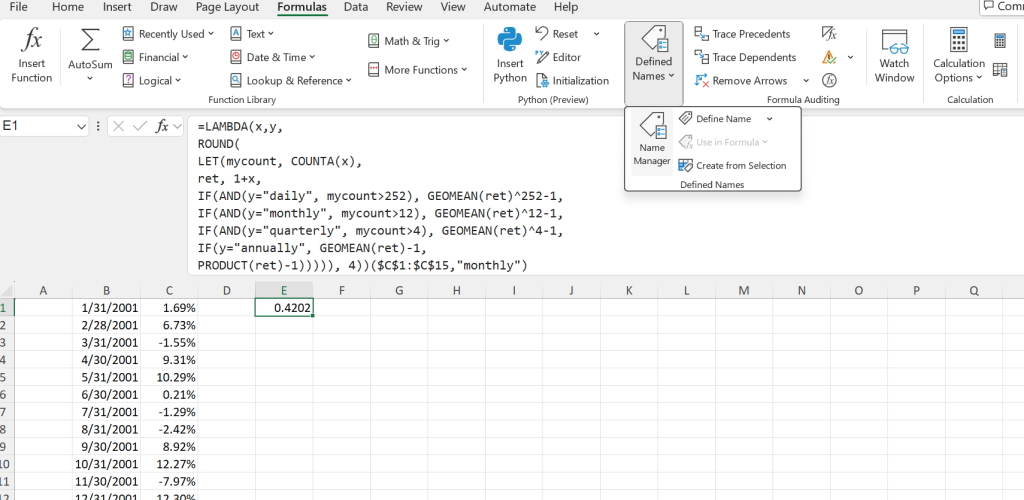
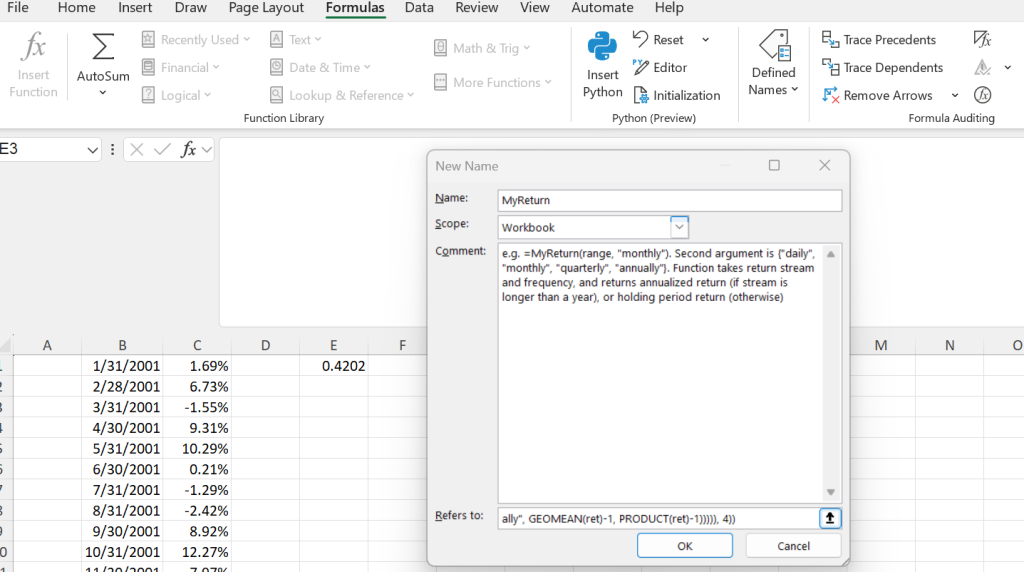
Finally, the full power of LAMBDA can be brought to life via the name manager. In the top ribbon to Excel, we go to Formulas -> Defined Names -> Name Manager -> New. We then paste our LAMBDA function (less than trailing ($C$1:$C$15,"monthly")) to “Refers to:”, and name our function MyReturns.

Figure 6a-6b: Using Name Manager To Create User Defined Function From LAMBDA

Now, anywhere in the sheet, we can call =MyReturns(return_range, frequency) and get our desired result. A lot cleaner than copying the formula in Figure 4 and editing the ranges in a few places each time you want a new return!

Figure 7: Calling Our User Defined Function

Max Drawdown

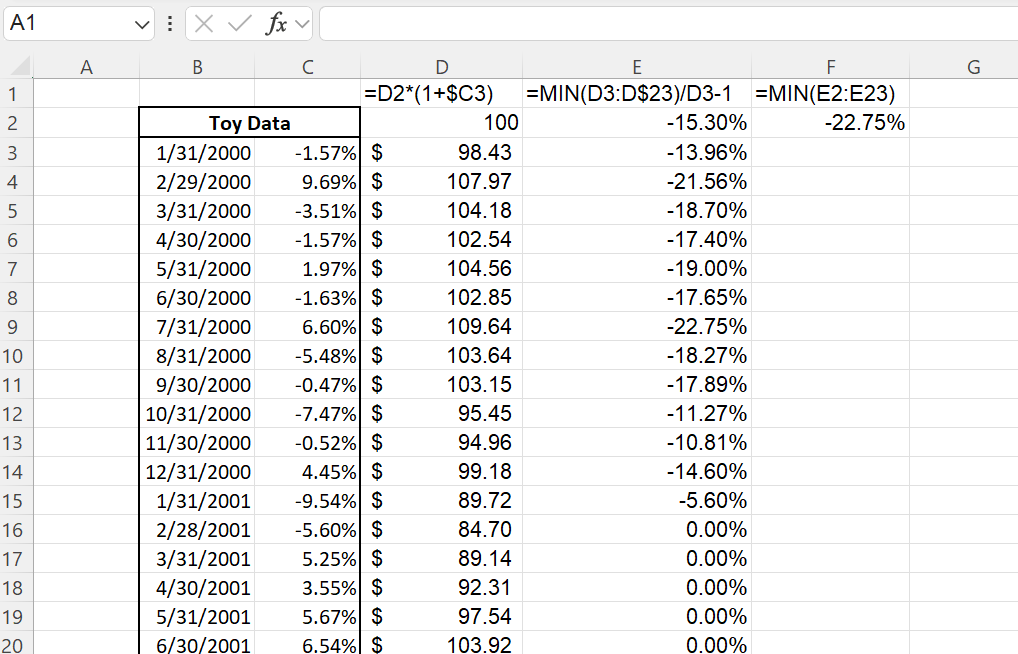
Let’s move to a more difficult analysis. Suppose we’d like to calculate the maximum drawdown of a return stream. If we’re doing this by hand, we’d likely need two helper columns: one to mimic the growth of $x invested in the instrument at the outset, and another to look at largest drawdown for each individual period in the accumulated growth. The minimum of these drawdowns is the maximum drawdown (see Figure 8). Can we wrap these two helper columns inside a single formula?

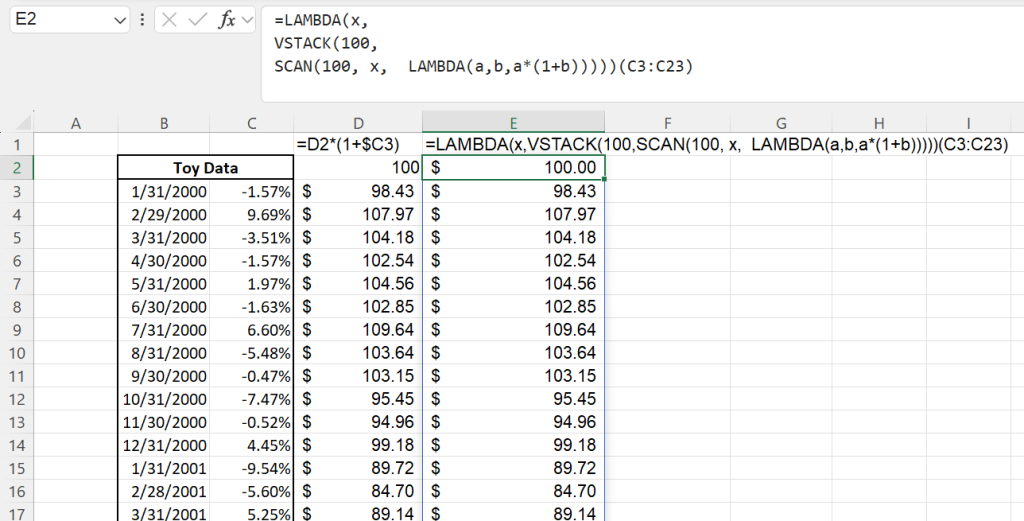
Figure 8: Calculating The Max Drawdown With Helper Columns

We can begin by replicating the growth of $100 (column D in Figure 8) using SCAN. Scan takes three arguments: an initial value, an array, and a LAMBDA which is applied to each element in the (accumulated) array. Take the following example. We want to find the cumulative sum of an array {1,2,3} in cells A1:A3. Our initial value is not the first value of the array, A1, but zero (this explanation makes clear in a few sentences why that’s the case). Our array is A1:A3. Our LAMBDA is of the form LAMBDA(a, b, a+b); a is the accumulating value, b is the value from our array, and a+b is the sum of the two. So the first “iteration” of SCAN has a=0 (the initial value we set), b=1 (the first value in our array), and so a+b=1. Our next iteration of SCAN takes the returned result as our new “accumulator”. So on the next iteration, we have a=1, b=2, and so a+b=3. Applying this to the problem at hand, we want our initial accumulator to be 100, our array to be an array of returns, and our LAMBDA to find the product of our accumulated value and the next monthly return. 

=SCAN(100, C3:C23, LAMBDA(a, b, a*(1+b)))

To include our initial investment, we can use VSTACK to append 100 at the top of our array.

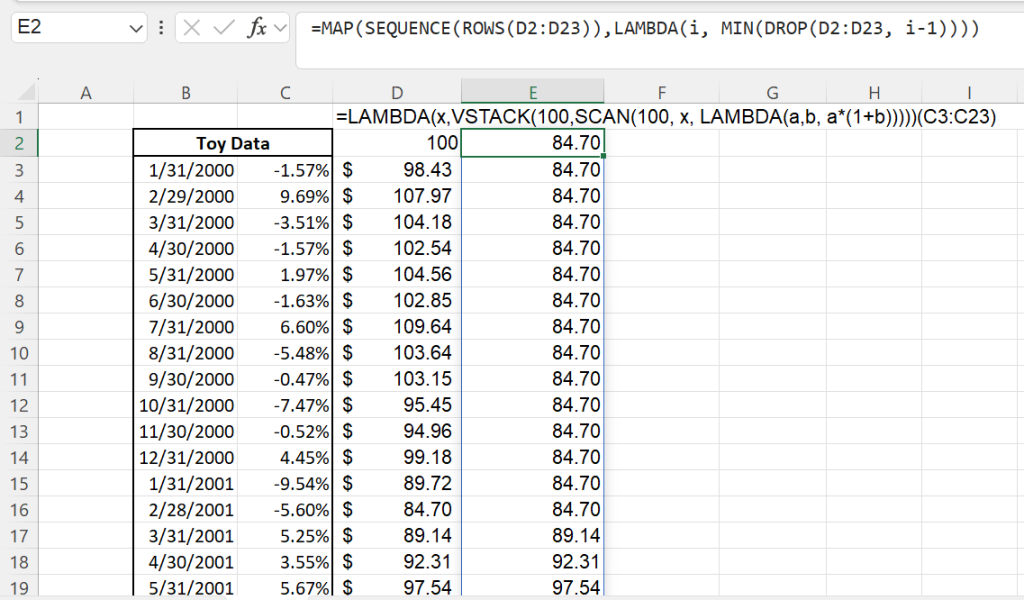
Figure 9: Using SCAN To Get Array Of Cumulative Growth

Using this array, we can return another array of the running minimum. To do so we use MAP and DROP in tandem. DROP simply returns an array less a specified number of rows. For example, =DROP(TRANSPOSE({1,3,5,7,9}),2) returns {5,7,9} and =DROP(TRANSPOSE({1,3,5,7,9}),-2) returns {1,3,5}. On the other hand, MAP works by passing each value of an array individually into a LAMBDA. For example, =MAP({1,3,5}, LAMBDA(i, 2*i)) returns {2,6,10}. We use MAP to pass a sequential list of values (corresponding to the rows in our array) into the DROP function, first dropping the first row, then the first two rows, etc. For each newly created array, we find the minimum. Our formula is: =MAP(SEQUENCE(ROWS(D3:D23)),LAMBDA(i, MIN(DROP(D3:D23, i-1)))).

Figure 10: Using MAP And Drop To Get Running Minimum

With the cumulative return and running minimum in hand, we can throw them in a LET, and divide element-wise to get the drawdowns at each period, and then find the minimum of this array. In total, our formula is:

=LAMBDA(x,
ROUND(LET(
cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
MIN(perdec)),
4))(C3:C23)

Time To Recovery

One more display of LAMBDA. In the same example as above, suppose we’d like to find the time to recovery (that is, the number of periods from the max drawdown point to a new high-water mark). From the maximum drawdown section, we already have arrays for the the cumulative growth, the running minimum, and the maximum decline from each period. In the below figure, we highlight in yellow the low point of the maximum drawdown ($84.70 in the cumulative growth array), the point where the drawdown begins ($109.64 in the cumulative growth array), and the point where the drawdown is fully recovered from ($110.93 in the cumulative growth array). Our ultimate task is to count the number of periods from when the drawdown hits its low ($84.70) to when the drawdown is fully recovered from ($110.93). We start by finding the peak-to-trough time, which is the number of periods from when the drawdown begins ($109.64) to when the drawdown reaches its nadir ($84.70).

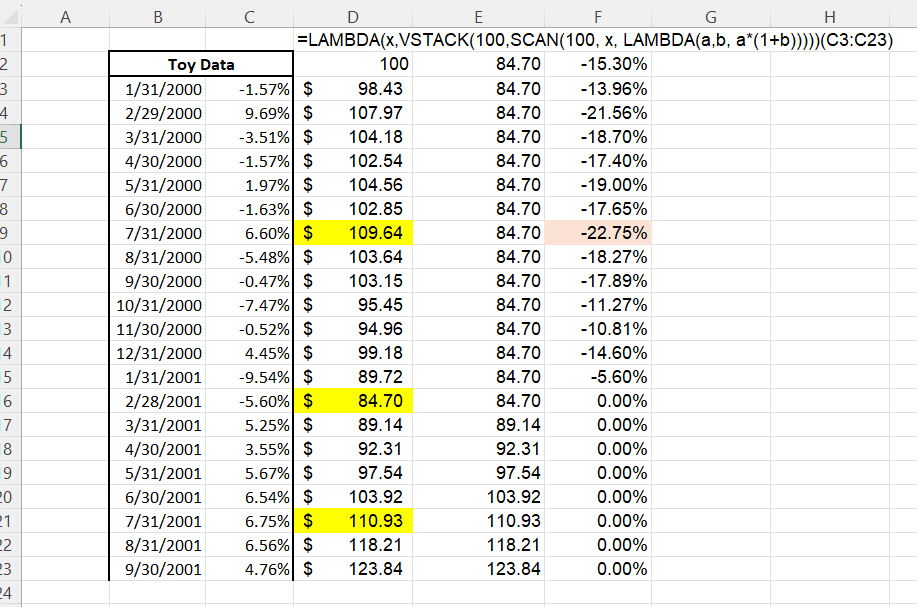
Figure 11: The Three Arrays Currently In LET

The toy example in the figure above hides a bit of the complexity in robustly completing this task. We start by returning the row where the maximum drawdown begins by MATCHing the maximum drawdown (the -22.75%) to its position in the drawdown array. From how the drawdown array (perdec in the LET) is calculated, this is the row when the drawdown starts (the “high-water” mark). With the row in hand, we can INDEX the cumulative return column to see the actual “high-water” value. So far, our code has evolved to the following:

=LAMBDA(x,
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
peak_row, MATCH(mydd, perdec, 0),
peak_dollar, INDEX(cumret, peak_row),
peak_dollar)

#in addition to the three arrays in Figure 11....
#...we have the peak_row as 8, and the peak_dollar as 109.64#

As the array of our running minimum is necessarily increasing, whatever the running minimum is at the row where the maximum drawdown occurs is the nadir of our drawdown period. Note that finding this value is very different from finding the minimum of the cumulative growth! For example, when starting at 100, decreasing to 99, increasing to 200, and then decreasing to 150, the maximum drawdown is the period 200 to 150, not 100 to 99. In contrast to finding the high-water mark, finding the subsequent low-point starts by finding the value of the cumulative growth, and then backing out the row. Our function is now:

=LAMBDA(x,
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
peak_row, MATCH(mydd, perdec, 0),
peak_dollar, INDEX(cumret, peak_row),
trough_dollar, INDEX(runmin, peak_row),
trough_dollar)

#we have the three arrays in Figure 11...#
#... that the peak dollar before the drawdown is 109.64...#
#... that 109.64 happens in the 8th period....#
#... and that the trough_dollar is 84.70.#

There is subtlety in finding the corresponding row in which the low-point occurs. We cannot simply INDEX, as the low-point’s dollar could have occurred earlier in the array (e.g. if you start with 100, decrease to 99, increase to 200, and decrease back to 99, the fourth row, not the second, is the low-point). Instead we use FILTER to return all the rows in our cumulative return array that have the low-point dollar and that occur after the high-point, before finding the minimum of these values. To make the formula cleaner, we add in a sequence of rows to the LET. In total, our function is:

=LAMBDA(x,
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
myrows, SEQUENCE(ROWS(cumret)),
peak_row, MATCH(mydd, perdec, 0),
peak_dollar, INDEX(cumret, peak_row),
trough_dollar, INDEX(runmin, peak_row),
trough_row, MIN(FILTER(myrows, (cumret=trough_dollar)*(myrows>peak_row))),
trough_row))

The above formula has all the necessary components to compute the peak-to-trough time (simply subtract the row where the “peak” occurs from the row where the “trough” occurs). The same sort of FILTER that was used to get the period when the trough occurs is used to get the period when the recovery occurs. Our final formula is below. 

=LAMBDA(x,
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
myrows, SEQUENCE(ROWS(cumret)),
peak_row, MATCH(mydd, perdec, 0),
peak_dollar, INDEX(cumret, peak_row),
trough_dollar, INDEX(runmin, peak_row),
trough_row, MIN(FILTER(myrows, (cumret=trough_dollar)*(myrows>peak_row))),
recover_row, MIN(FILTER(myrows, (cumret>peak_dollar)*(myrows>trough_row))),
recover_row-trough_row))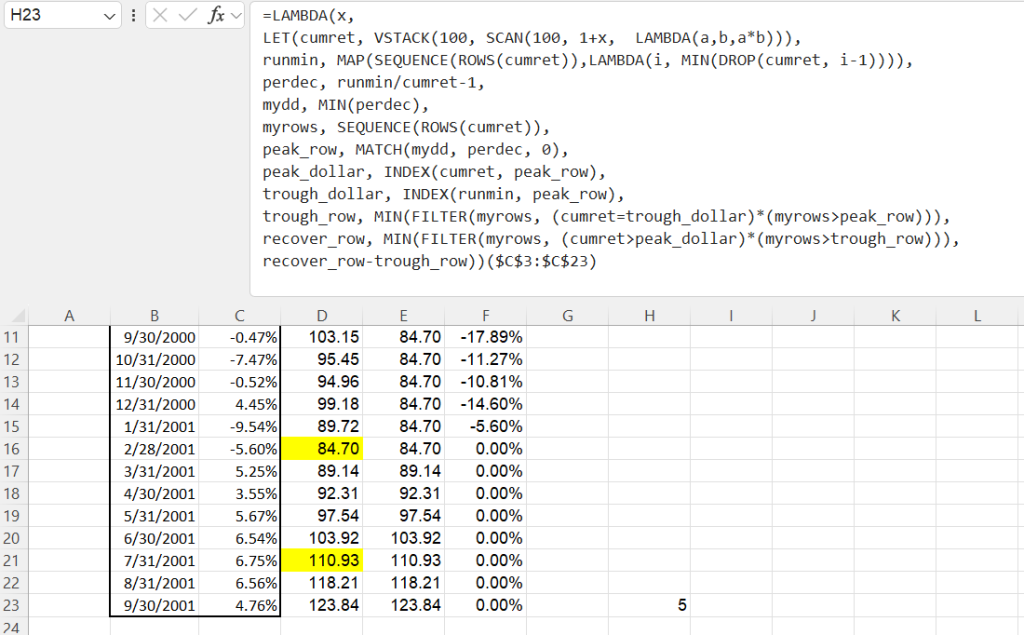
Figure 12: Computing The Time To Recovery

LAMBDA of LAMBDAs

Once LAMBDA functions are in the name manager, one can also use them in defining other LAMBDAs. For example, once I have a LAMBDA to compute the return and volatility of a stream of returns, I can make a nicer presentation of the results, adding headers, titles, and pseudo-margins. 

=LAMBDA(x,y,
VSTACK(
{"********","","REALIZED","","********"},
{"","Return","","Volatility",""},
HSTACK("", MyReturn(x,y), "", MyVol(x,y), ""),
IF(SEQUENCE(1,5)<6, "********")))($C$3:$C$23,"monthly")

#MyReturn and MyVol are the previously defined LAMBDAs#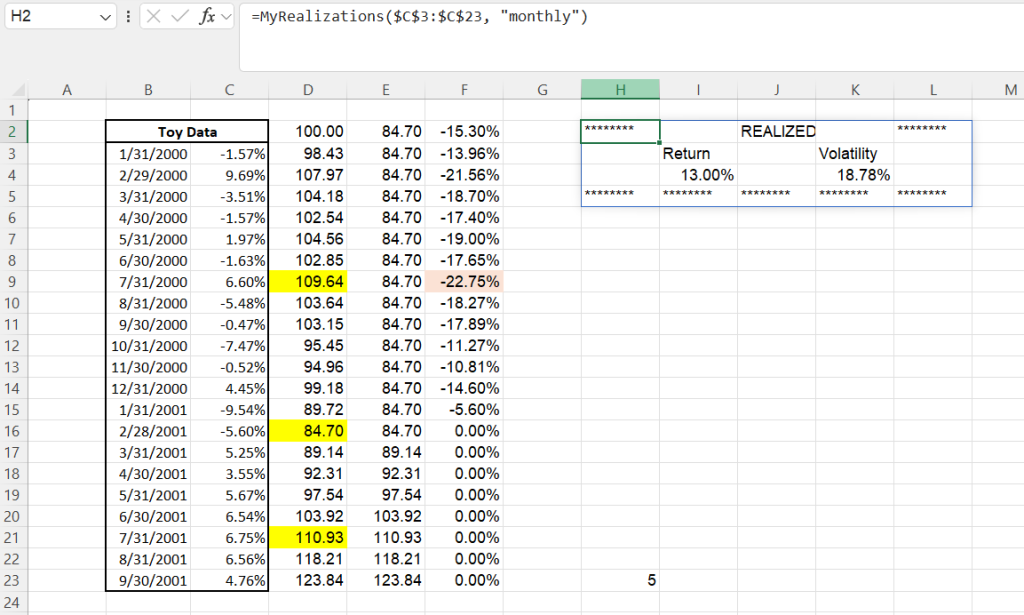
Figure 13: Displaying Realizations

We can group other similar measures together as well. For example distributional measures:

=LAMBDA(x,
IFERROR(
LET(mainheader, {"********","SAMPLE","","DIST","********"},
header1, {"Min","Q1","Median","Q3","Max"},
headers2, {"Mean","SD","Skew","Kurtosis (excess)",""},
space, IF(SEQUENCE(1,5)<6, "", ""),
footer, IF(SEQUENCE(1,5)<6, "********"),
VSTACK(mainheader, header1, MyDist(x), space, headers2, MyMoments(x), footer)),""))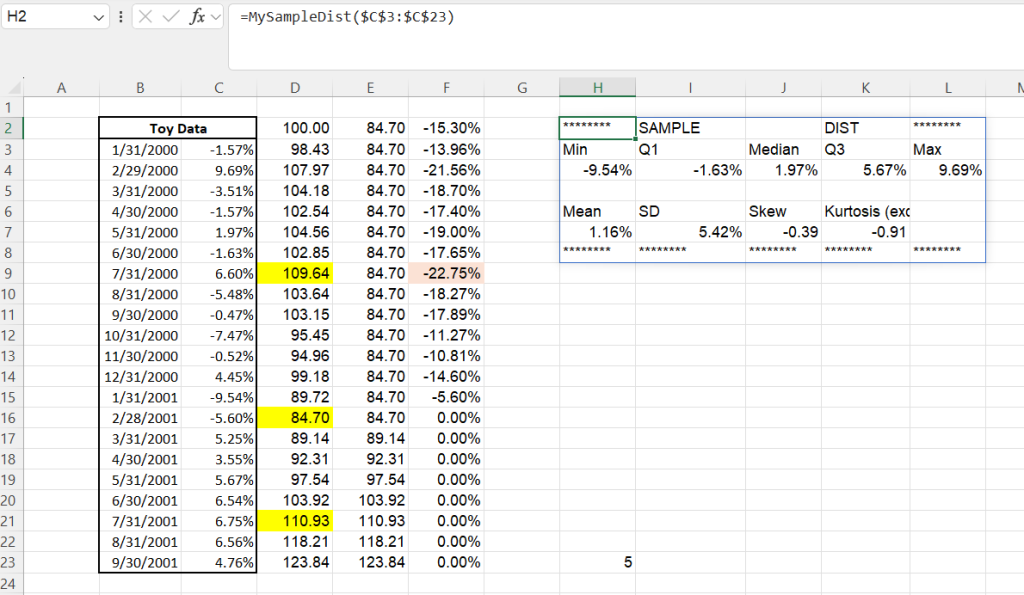
Figure 14: Displaying Distributional Metrics

Or Path-dependent measures:

=LAMBDA(x,
VSTACK(
{"********","PATH","","SPECIFIC","********"},
{"","Max Drawdown","Peak To Trough Periods","Time To Recovery Periods",""},
HSTACK("",MyDD(x), MyPtT(x), MyTTR(x),""),
IF(SEQUENCE(1,5)<6, "********","")))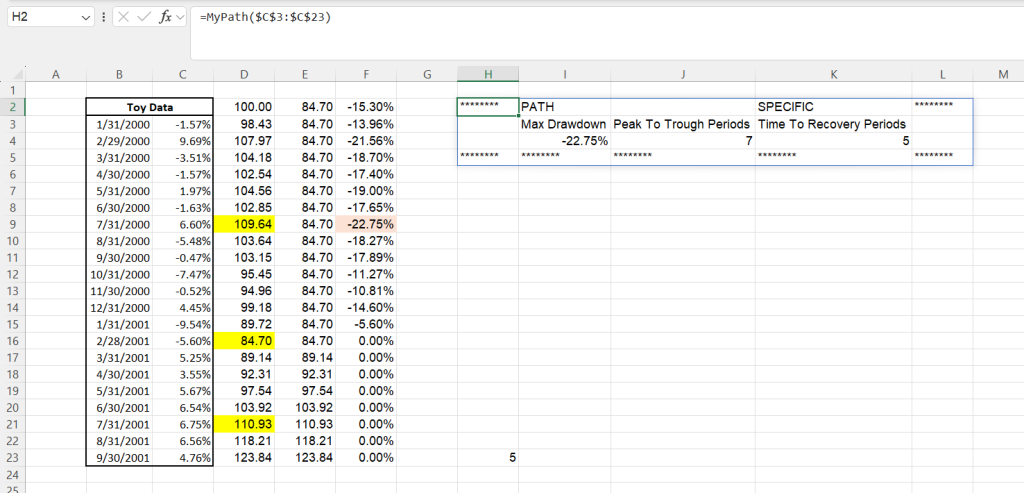
Figure 15: Path-Specific Metrics

Or even displaying all three– annualized realizations, distributional metrics, and path-specific metrics– in one go!

=LAMBDA(returns,frequency,
IFERROR(VSTACK(
MyRealizations(returns, frequency),
IF(SEQUENCE(1,5)<6, "",""),
MySampleDist(returns),
IF(SEQUENCE(1,5)<6, "",""),
MyPath(returns)),""))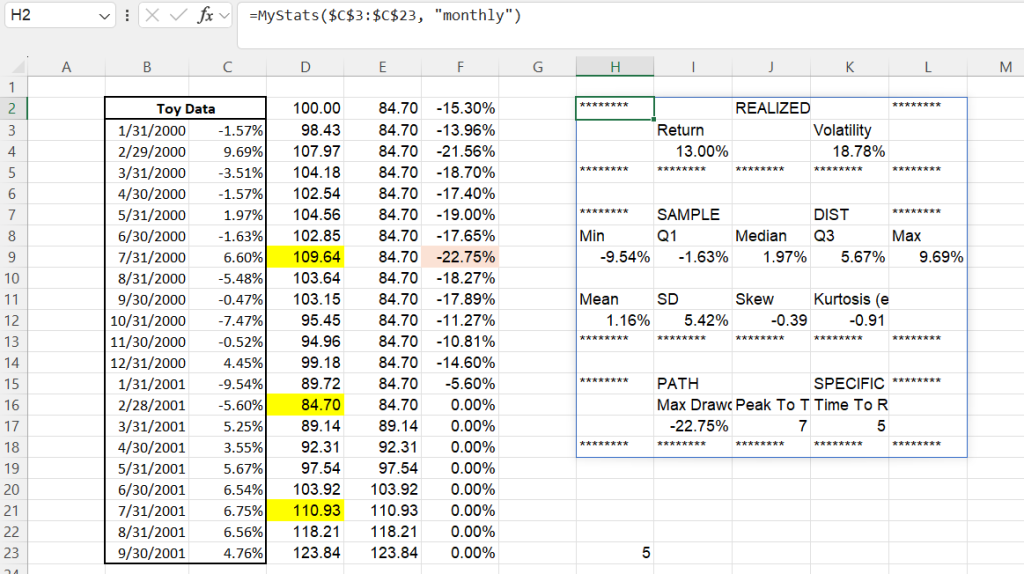
Figure 16: Return Overview

Default Excel Settings

I always want Excel to open with the same layout and user-defined functions loaded. The functions I want are listed below, and settings I want are Calibri 11 font, 80% zoom, five sheets labeled “UDFs”, “README”, “RawData”, “Analysis”, and “Output”, as well as the first two rows and columns “frozen” in each sheet (click on cell C3, then View -> “Freeze Panes” -> “Freeze Panes”).

Once I have all the above settings set, I can get new Excel sheets to open with the same settings by saving the file as an “Excel Template” named “Book” in C:\Users\name\AppData\Roaming\Microsoft\Excel and then restarting Excel.

DateToNum:

=LAMBDA(x, 
NUMBERVALUE(YEAR(x)&IF(MONTH(x)<10, "0"&MONTH(x), MONTH(x))&IF(DAY(x)<10, "0"&DAY(x), DAY(x))))

#e.g. =DateToNum("01/02/2003") returns 20030102#

NumToDate:

=LAMBDA(x,
LET(y, LEFT(x,4),
m, MID(x,5,2),
d, RIGHT(x,2),
IF(LEN(x)=8, DATE(y,m,d), DATE(y,m,1))))

#e.g. =NumToDate(20030102) gives "01/02/2003" (well, really the number of days since 01/01/1970, but that's just formatting)#

MyReturn:

=LAMBDA(range,frequency,
ROUND(
LET(mycount, COUNTA(range),
ret, 1+range,
IF(AND(frequency="daily", mycount>252), GEOMEAN(ret)^252-1,
IF(AND(frequency="monthly", mycount>12), GEOMEAN(ret)^12-1,
IF(AND(frequency="quarterly", mycount>4), GEOMEAN(ret)^4-1,
IF(frequency="annually", GEOMEAN(ret)-1,
PRODUCT(ret)-1))))), 4))

#e.g. =MyReturn(range, "monthly"). Frequency is {"daily", "monthly", "quarterly",  "annually"}. Gives annualized return (if the return stream lasts longer than a year), or holding period return (if less than a year).#

MyVol:

=LAMBDA(range,frequency,
ROUND(
LET(mycount, COUNTA(range),
IF(frequency="daily", STDEV(range)*SQRT(252),
IF(frequency="monthly", STDEV(range)*SQRT(12),
IF(frequency="quarterly", STDEV(range)*SQRT(4),
STDEV(range))))),4))

#e.g. =MyVol(range, "daily"). The frequency is {"daily", "monthly", "quarterly", "annually"}. Gives annualized standard deviation.#

MyDD:

=LAMBDA(x,
ROUND(
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
mydd),4))

#Given a sequential return stream, returns the maximum cumulative drawdown.#

My PtT:

=LAMBDA(x,
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
myrows, SEQUENCE(ROWS(cumret)),
peak_row, MATCH(mydd, perdec, 0),
peak_dollar, INDEX(cumret, peak_row),
trough_dollar, INDEX(runmin, peak_row),
trough_row, MIN(FILTER(myrows, (cumret=trough_dollar)*(myrows>peak_row))),
trough_row-peak_row))

#The number of periods from Peak to Trough#

MyTTR:

=LAMBDA(x,
LET(cumret, VSTACK(100, SCAN(100, 1+x,  LAMBDA(a,b,a*b))),
runmin, MAP(SEQUENCE(ROWS(cumret)),LAMBDA(i, MIN(DROP(cumret, i-1)))),
perdec, runmin/cumret-1,
mydd, MIN(perdec),
myrows, SEQUENCE(ROWS(cumret)),
peak_row, MATCH(mydd, perdec, 0),
peak_dollar, INDEX(cumret, peak_row),
trough_dollar, INDEX(runmin, peak_row),
trough_row, MIN(FILTER(myrows, (cumret=trough_dollar)*(myrows>peak_row))),
recover_row, MIN(FILTER(myrows, (cumret>peak_dollar)*(myrows>trough_row))),
recover_row-trough_row))


#The number of periods from Trough back to high-water mark#

MyMoments:

=LAMBDA(x,
ROUND(
HSTACK(AVERAGE(x), STDEV(x), SKEW(x), KURT(x)),4))

#Gives the first four moments of the distribution of returns#

MyDist:

=LAMBDA(x,
ROUND(
HSTACK(MIN(x), QUARTILE(x, 1), QUARTILE(x, 2), QUARTILE(x,3), QUARTILE(x,4)),
4))

#Gives the min, Q1, median, Q3, and max of a given sequence#

MyRealizations:

=LAMBDA(x,y,
  VSTACK(
     {"********","","REALIZED","","********"},
     {"","Return","","Volatility",""},
     HSTACK("", MyReturn(x,y), "", MyVol(x,y), ""),
    IF(SEQUENCE(1,5)<6, "********")
   ))

#e.g. =MyRealizations(range, "quarterly"). Given a return stream and frequency ({"Daily", "Monthly", "Quarterly", "Annually"}), displays the return and volatility#

MySampleDist:

=LAMBDA(x,
IFERROR(
LET(mainheader, {"********","SAMPLE","","DIST","********"},
    header1, {"Min","Q1","Median","Q3","Max"},
    headers2, {"Mean","SD","Skew","Kurtosis (excess)",""},
    space, IF(SEQUENCE(1,5)<6, "", ""),
   footer, IF(SEQUENCE(1,5)<6, "********"),
    VSTACK(mainheader, header1, MyDist(x), space, headers2, MyMoments(x), footer)),
""))

#Gives distributional measures of return stream#

MyPath:

=LAMBDA(x,
VSTACK(
    {"********","PATH","","SPECIFIC","********"},
    {"","Max Drawdown","Peak To Trough Periods","Time To Recovery Periods",""},
    HSTACK("",MyDD(x), MyPtT(x), MyTTR(x),""),
    IF(SEQUENCE(1,5)<6, "********","")))

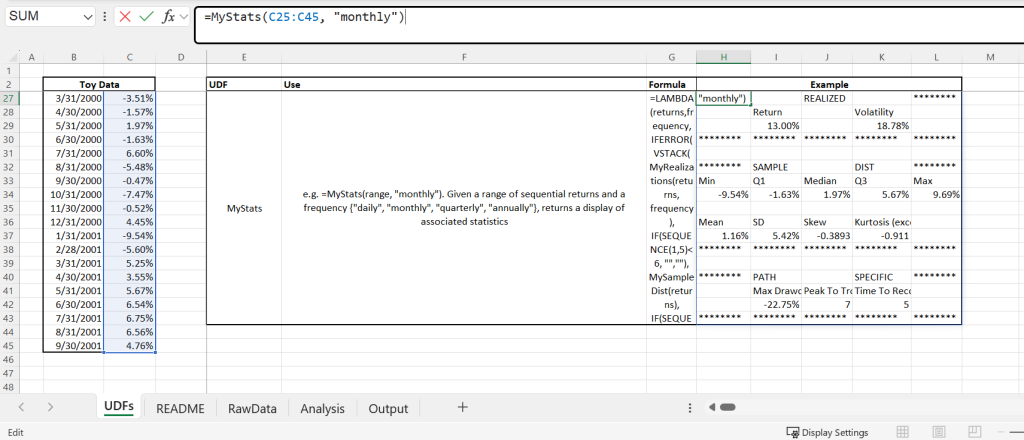
#Gives path-specific metrics: max drawdown, peak-to-trough, and time to recovery#

MyStats:

=LAMBDA(returns,frequency,
IFERROR(VSTACK(
MyRealizations(returns, frequency),
IF(SEQUENCE(1,5)<6, "",""),
MySampleDist(returns),
IF(SEQUENCE(1,5)<6, "",""),
MyPath(returns)),""))

#e.g. =MyStats(range, "monthly"). Given a range of sequential returns and a frequency {"daily", "monthly", "quarterly", "annually"}, returns a display of associated statistics#

The output array from MyStats is shown in an example below.

Figure: Example Output From MyStats UDF